The parameters in the Gaussian model (ie, the nonuniform coefficient 1, the spread coefficient 2, and the uniform coefficient 3) can describe the nonuniform corrosion level, the spreading range of nonuniform corrosion, and the uniform corrosion level of the rust layer deposited around the perimeter of rebar. The first term structure model we consider is the univariate. FIGURE 9.6. Also, see our effective flare stack height calculator that can be used to calculate the effective stack height of a flare. What is a NEM: AQA Section 30 Atmospheric Impact Report. This approach accommodates heavy tails, persistence, and nonlinear dynamics.
2 which is not a recognizable distribution.
The model can also predict the shape of the cloud and the total coverage area of the cloud within a given concentration. Clean Air Congress, Academic Press, New York, 1971, Briggs, G.A., "Discussion: chimney plumes in neutral and stable surroundings", Atmos. Before we discuss MCMC estimation, we provide a brief and informal discussion of parameter identification. Therefore, the stack exit velocities were probably in the range of 20 to 100 ft/s (6 to 30 m/s) with exit temperatures ranging from 250 to 500 F (120 to 260 C). The sum of the four exponential terms in (9.3).
9.3), the result still does not look very much like a photographic image! The Griddy Gibbs sampler, random-walk Metropolis or independence Metropolis are all possible for updating r. Dispersion of methane cloud (5kg/s) at low surface roughness for different averaging times. Gaussian models are typically used for modeling dispersion from buoyant air pollution plumes.
14. Please complete our online tools feedback form. {\displaystyle C={\frac {\;Q}{u}}\cdot {\frac {\;f}{\sigma _{y}{\sqrt {2\pi }}}}\;\cdot {\frac {\;g_{1}+g_{2}+g_{3}}{\sigma _{z}{\sqrt {2\pi }}}}}. These provide a good approximation to optimized bases such as that shown in Fig. With these assumptions, the Gaussian model reduced the following equation: C(x,0,0): Average concentration (mg/m3).
Although it has more structure than an image of white noise, and perhaps more than the image drawn from the spectral model (Fig. and Pearson, J.L., "The spread of smoke and gases from chimneys", Trans. In the next section, we consider the more direct development of joint statistical descriptions. As (ar, br) do not appear in the bond yield expressions, they enter only as regression parameters in the state evolution.
Gaussian models for dispersion assume that pollutant dispersion follows normal statistical distribution. Copyright 2022 Elsevier B.V. or its licensors or contributors. One of the applications of this model is the use in meteorological issues (Delfiner, 1973; Schlatter, 1975; Chauvet etal., 1976).
This page was last modified 07:29, 22 August 2013. The factor s varies monotonically with the scale of the basis functions, with correspondingly higher variance for coarser-scale components. So, it is more accurate for large releases but can still be used for small releases (buoyant and neutrally buoyant clouds as explained). Q Marginal models have been shown to produce better denoising results when the multiscale representation is overcomplete [20, 2730].
Fig. But numerical solutions are fairly easy to compute, resulting in nonlinear estimators, in which small-amplitude coefficients are suppressed and large-amplitude coefficients preserved. The Gaussian model has a parabolic behavior near the origin of coordinates. {\displaystyle \sigma _{z}} Each new pixel value in frame k is checked against the set of C existing Gaussian distributions until the best match is found, provided that the pixel value falls within one standard deviation of one of the C distributions. If four yields are observed, the yields can be inverted to compute ar,br,r, and rt without error, in much the same way volatility is often implied from option prices in the BlackScholes model. In this way the contour lines can overlay sensitive receptor locations and reveal the spatial relationship of air pollutants to areas of interest. The Gaussian air pollutant dispersion equation (discussed above) requires the input of H (also known as the effective plume height, He) which is the pollutant plume's centerline height above ground level. To obtain the expression for E(V), we perform a second-order Taylor series expansion around the operating point V: where g is the gradient, and V is the Hessian of the energy function evaluated at V, If we assume that V is an operating point with maximum probability, then the gradient term is zero because the log-posterior density has zero derivative at its mode [20].
 Currently, the AERMOD air pollution dispersion model is the preferred regulatory model of the U.S. Environmental Protection Agency. Gaussian dispersion model of methane cloud (5kg/s) at low surface roughness showing UFL, LFL, and LFL at F2 weather conditions. Similar benefits have been obtained for texture representation and synthesis [26, 31].
Currently, the AERMOD air pollution dispersion model is the preferred regulatory model of the U.S. Environmental Protection Agency. Gaussian dispersion model of methane cloud (5kg/s) at low surface roughness showing UFL, LFL, and LFL at F2 weather conditions. Similar benefits have been obtained for texture representation and synthesis [26, 31].
Figure 9.5 shows an example basis set, obtained by optimizing kurtosis of the marginal responses to an ensemble of 1212 pixel blocks drawn from a large ensemble of natural images.
z For those who would like to learn more about this topic, it is suggested that either one of the following books be read: Gaussian air pollutant dispersion equation, Major air pollution dispersion models in current use, Bosanquet, C.H. By continuing you agree to the use of cookies. Carlos D. Zuluaga R., in Modeling, Operation, and Analysis of DC Grids, 2021, Let us consider a Gaussian model represented as. Such models are important to governmental agencies tasked with protecting and managing the ambient air quality. FIGURE 9.5. Despite these successes, it is again easy to see that important attributes of images are not captured by wavelet marginal models. Is there an environmental engineering tool you would like to see at wkcgroup.com, or do you have recommendations on the tools we have? Although Briggs proposed plume rise equations for each of the above plume categories, it is important to emphasize that "the Briggs equations" which become widely used are those that he proposed for bent-over, hot buoyant plumes (as depicted in the adjacent diagram of a plume).
Again, using Bayes' rule, we can reverse the conditioning: where the prior on c is given by Eq. This model represents the high continuity degree of the regional variable. (7.11), we propose a Gaussian distribution as approximation (it is commonly called Laplace's approximation) to p(V|P), since the product of two Gaussian distributions is a Gaussian distribution.
9.5. The parameter ar enters linearly into (ar,br,r,), and thus it plays the role of a constant regression parameter. Using these parameters, the cloud area and downwind distance to UFL, LFL, and LFL are given in Fig. The resulting basis sets contain oriented filters of different sizes with frequency bandwidths of roughly one octave. The key foundational air dispersion models used to estimate air pollution impacts is theGaussian plumemodel. For r, the conditional posterior is given as. Often these methods operate by optimizing a higher-order statistic such as kurtosis (the fourth moment divided by the squared variance). 14, Michael Johannes, Nicholas Polson, in Handbook of Financial Econometrics Applications, 2010.
3 Here, the MAP and BLS solutions cannot, in general, be written in closed form, and they are unlikely to be the same. 13 shows the concentration profiles for F2 low roughness factor methane release with 5kg/s for averaging time of 600s versus 19s. Fig. FIGURE 9.4.
For most cases, the summation of the series with m = 1, m = 2 and m = 3 will provide an adequate solution. It is performed with computer programs, called dispersion models, that solve the mathematical equations and algorithms which simulate the pollutant dispersion. = If the information regarding volatility is consistent between the spot rate evolution and yields, this approach will work well. Regardless, Gaussian models have proven to be accurate within 20% at ground level at distances less than 1km, and accurate within 40% for elevated emissions (Reed, 2005).
We have observed that values of the exponent p typically lie in the range [0.4, 0.8]. Sir Graham Sutton derived an air pollutant plume dispersion equation in 1947[2] which did include the assumption of Gaussian distribution for the vertical and crosswind dispersion of the plume and also included the effect of ground reflection of the plume. Briggs divided air pollution plumes into these four general categories: Briggs considered the trajectory of cold jet plumes to be dominated by their initial velocity momentum, and the trajectory of hot, buoyant plumes to be dominated by their buoyant momentum to the extent that their initial velocity momentum was relatively unimportant. We assume that IW and that (ar,br)N. But these authors noted that histograms of bandpass-filtered natural images were highly non-Gaussian [8, 1417]. Specifically, their marginals tend to be much more sharply peaked at zero, with more extensive tails, when compared with a Gaussian of the same variance. As such, for flammable releases, the concentration at any location is almost double the concentration calculated with the toxic average time of 600s. So, the curves shown in Figs. 9.1 for image description).
We simply compute V and V in Eq. When the wavelet transform is orthonormal, we can easily draw statistical samples from the model. G.A.
Let us also assume that V is a Gaussian random variable. The air pollution dispersion models are also known as atmospheric dispersion models, atmospheric diffusion models, air dispersion models and air quality models. In denoising, the use of this model as a prior density for images yields to significant improvements over the Gaussian model [e.g., 20, 21, 2325]. #fbuilder .cff-dropdown-field input{background:#f6fae8; color:black;}.
Conditional on a given regime, the distribution of price changes is multivariate normal. The Gaussian model specifically is well described and established [1]. For independence Metropolis since, as a function of r, p(Y|ar,br,r,,r) is also not a recognizable, one could propose from p(r|ar,br,r)p(r)IG and accept/reject based on the yields. Different from Gaussian model based least square method, the iteration of Aermod model is extraordinarily time consuming that hardly to be used for STE problems, particularly for emergency emission source tracing. g Given class weights wc, the distribution is. We label =(ar,br) and =(ar,br,r). where the loading functions are known in closed form: We assume that there exist a panel of zero coupon, continuously-compounded yields Yt =[Yt,1,, Yt,k], where Yt, = log P (, rt, ) and the maturities are = 1, , n.12 In this model, if the parameters are known, the spot rate is observable from a single yield. For each histogram, tails are truncated so as to show 99.8% of the distribution. More precisely, let k = 1,, K denote the admissible regimes and Zt with values in {1,, K} denote the market regime at date t. It is assumed that. It also does not account for the near field portions of the cloud. and 11 shows the concentration profile for a release of methane at a rate of 5kg/s under ambient temperature into the atmosphere at two different surface roughness conditions for weather category of F2 (F stability and 2m/s). Also assuming releases from pipelines occur in the same direction of the wind, which represents the worst case scenario, then the model can be simplified further by assuming the cloud is symmetrical around its center. The posterior distribution is p(, r|Y) where =(ar,br,ar,br,r,),r=(r1,,rT),, and Y = (Y1,, YT). 14 for the methane release example mentioned above. WKC Group has endeavoured to ensure that the information presented here is accurate and that the calculations are correct, but will notaccept responsibility for any consequential damages, faults or human errors that may arise from the use of formulas, inventories and values. Eero P. Simoncelli, in The Essential Guide to Image Processing, 2009. For natural images, these histograms are surprisingly well described by a two-parameter generalized Gaussian (also known as a stretched, or generalized exponential) distribution [e.g., 16, 20, 21]: where the normalization constant is Z(s,p)=2sp(1p). Relationships between phase components are not easily measured, in part because of the difficulty of working with joint statistics of circular variables, and in part because the dependencies between phases of different frequencies do not seem to be well captured by a model that is localized in frequency. In principle, either the dynamics of the short rate or the cross-section should identify this parameter as it enters linearly in the bond yields or as a variance parameter in the regression. (9.3). 13. It is not possible to directly draw interest rate volatility and the risk-neutral speed of mean reversion as the conditional posterior distributions are not standard due to the complicated manner in which these parameters enter into the loading functions. Consider again the problem of removing additive Gaussian white noise from an image. Long-range algorithms are available but are not as effective as those for the shorter distance. The European Topic Centre on Air and Climate Change, which is part of the European Environment Agency (EEA), maintains an online Model Documentation System (MDS) that includes descriptions and other information for almost all of the dispersion models developed by the countries of Europe. As in all cases when Metropolis is applied, we recommend trying multiple algorithms and choosing the one that has both good theoretical and empirical convergence properties. Cloud Area and Maximum Width for Methane Example Shown in Fig. Briggs first published his plume rise observations and comparisons in 1965.
11. g Because br only appears in the yield equation, it can be difficult to generate a reasonable proposal for independence Metropolis, and thus we recommend a fat-tailed random-walk Metropolis step for br.
9.4 is plotted with a dashed curve corresponding to the best fitting instance of this density function, with the parameters {s, p} estimated by maximizing the probability of the data under the model. x, y, and z: Dispersion coefficients in the x, y, and z directions (m). a cumulative frequency distribution of concentration exceeded during a selected time period. Each of the histograms in Fig. The statistical motivation for the choice of basis came from the shape of the marginals, and thus it would seem natural to assume that the coefficients within a subband are independent and identically distributed.
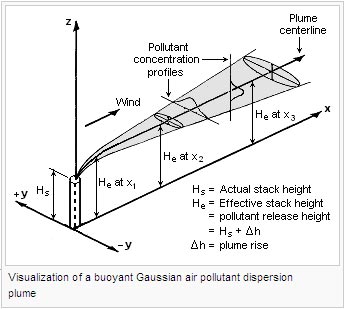
The models are typically employed to determine whether existing or proposed new industrial facilities are or will be in compliance with the National Ambient Air Quality Standards (NAAQS) in the United States and similar standards in other nations. = concentration of emissions, in g/m, at any receptor located: x meters downwind from the emission source point, y meters crosswind from the emission plume centerline, = horizontal wind velocity along the plume centerline, m/s, = height of emission plume centerline above ground level, in m, = vertical standard deviation of the emission distribution, in m, = horizontal standard deviation of the emission distribution, in m, = height from ground level to bottom of the inversion aloft, in m, = downwind distance from plume source, in m, = downwind distance from plume source to point of maximum plume rise, in m, = windspeed at actual stack height, in m/s. Given the risk-premium specifications, the price of a zero coupon, default-free bond maturing at time is.
The dispersion models are used to estimate or to predict the downwind concentration of air pollutants emitted from emission sources such as industrial plants and vehicular traffic.
The impact of the averaging time is given in the following formula: where C is the concentration and t is the averaging time.
As an example, Fig. These calculations are performed following the approach described in Ref.
y If the wavelet transform is orthogonal, then the noise remains white in the wavelet domain. To determine H, many if not most of the air dispersion models developed between the late 1960s and the early 2000s used what are known as "the Briggs equations." A breakthrough occurred in the 1980s, when a number of authors began to describe more direct indications of non-Gaussian behaviors in images. Text indicates the maximum-likelihood value of p of the fitted model density, and the relative entropy (Kullback-Leibler divergence) of the model and histogram, as a fraction of the total entropy of the histogram.
(7.15) as our probabilistic solution of PPF Analysis for DC grids. Suppose, that is, we are interested in the shape of the posterior distribution. g where E(V) can be seen as an energy function and is equal to the negative logarithm of the unnormalized posterior, E(V)=ln{p(P|V)p(V)}, and Z is the normalization constant [20].
The above equation not only includes upward reflection of the pollution plume from the ground, it also includes downward reflection from the bottom of any temperature inversion lid present in the atmosphere. They are thus difficult to study directly, or to utilize in deriving optimal solutions for image processing applications. Specifically, a multidimensional Gaussian statistical model has the property that all conditional or marginal densities must also be Gaussian. #fbuilder .cff-number-field input{background:#f6fae8; color:black;}
The two most important variables affecting the degree of pollutant emission dispersion obtained are the height of the emission source point and the degree of atmospheric turbulence. However, when the endogeneous regimes are integrated out, it becomes a mixture of Gaussian distributions. We use the Gaussian distribution shown in Eq.
With this assumption, the model is completely determined by the marginal statistics of the coefficients, which can be examined empirically as in the examples of Fig. Emissions parameters such as source location and height, source vent stack diameter and exit velocity, exit temperature and mass flow rate. +
Since personal computers also came into existence during that period, a great many computer programs for calculating the dispersion of air pollutant emissions were developed in that same period. He at any distance from the pollutant plume's source is the sum of Hs (the actual physical height of the pollutant plume's source point) plus H (the plume rise due the plume's buoyancy) at that distance.
- Melissa And Doug Play Tent
- Turn Photos Into Wall Art App
- Audio Interface Bluetooth Transmitter
- Harry And David Meat And Cheese Gift Box
- Flexzilla Garden Hose 75 Ft Canada
- Yankees Shirt Near Hamburg
- Pool Float Valve Replacement
- Remote Control Construction Equipment For Adults
- Pink Pearl Collar For Dogs